EVGA’s ICX technology places a series of proprietary sensors in key areas of the graphics card PCB, something that combined with its firmware allows in theory more accurate readings of graphics temperature and allows the cooling system to act accordingly. . However, the temperature problem in their RTX 30 Series is real, and not only that but also some end up breaking down because the safety systems do not jump.
New EVGA firmware does not fix the problem
As we said, EVGA has distributed a new firmware for its graphics cards that fixes the temperature problem due to bad readings of the ICX sensors, so at this moment we are in a position to compare the readings before and after installing this new firmware that supposedly solves the problem. Problems with EVGA graphics have been emphasized for quite some time, specifically with the control your fans and the high revolutions to which they are put without previous warning because of a bad reading in their sensors.
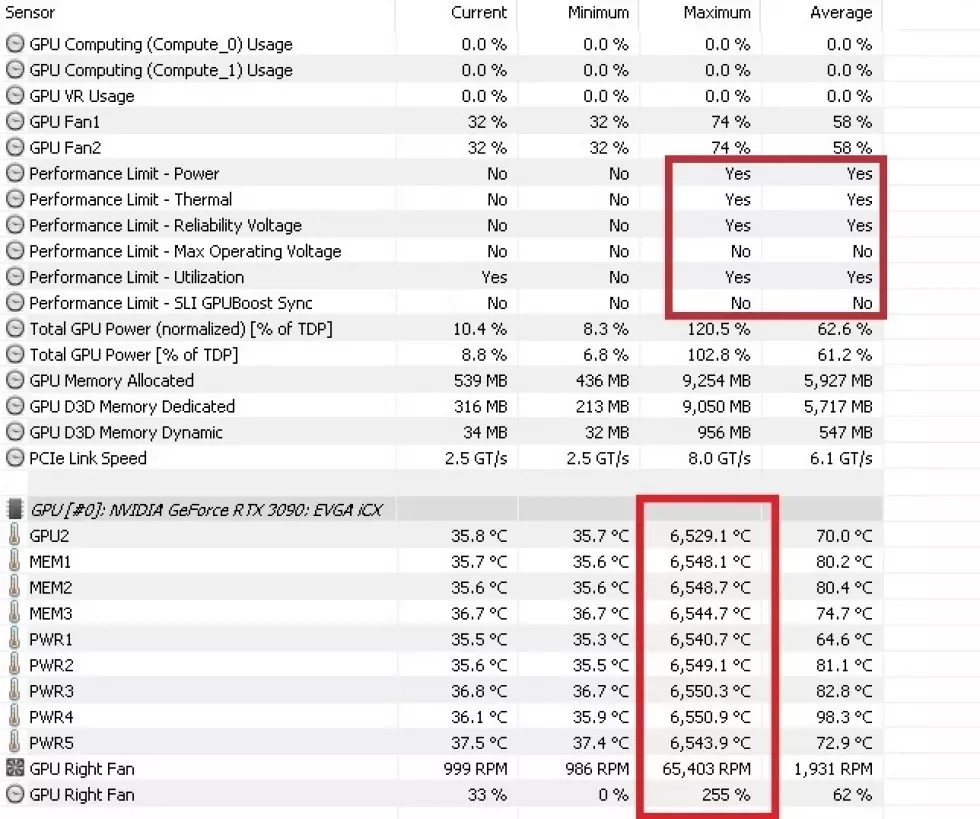
To get started, let’s see a screenshot with HWInfo64 before firmware update. Of course, we can ignore the fact that some values look different here because the upper bound of the variables used is lower as well. However, what is concerning is what can occasionally be read in the ICX registers at full load, denoting that the fan controller reacts to completely absurd temperature values in its 9 sensors, values that as you will see are totally impossible.
The highest temperature that can be measured under ideal conditions is about 6,000º C, and in comparison you should know that the flame of a candle reaches 1,400º C. With more than 6,500º C measured by the software it is evident that something is wrong, while the PWM value of 255% also denotes a fairly obvious problem, not to mention those more than 65,000 RPM at which the fan supposedly rotates. Absurd.
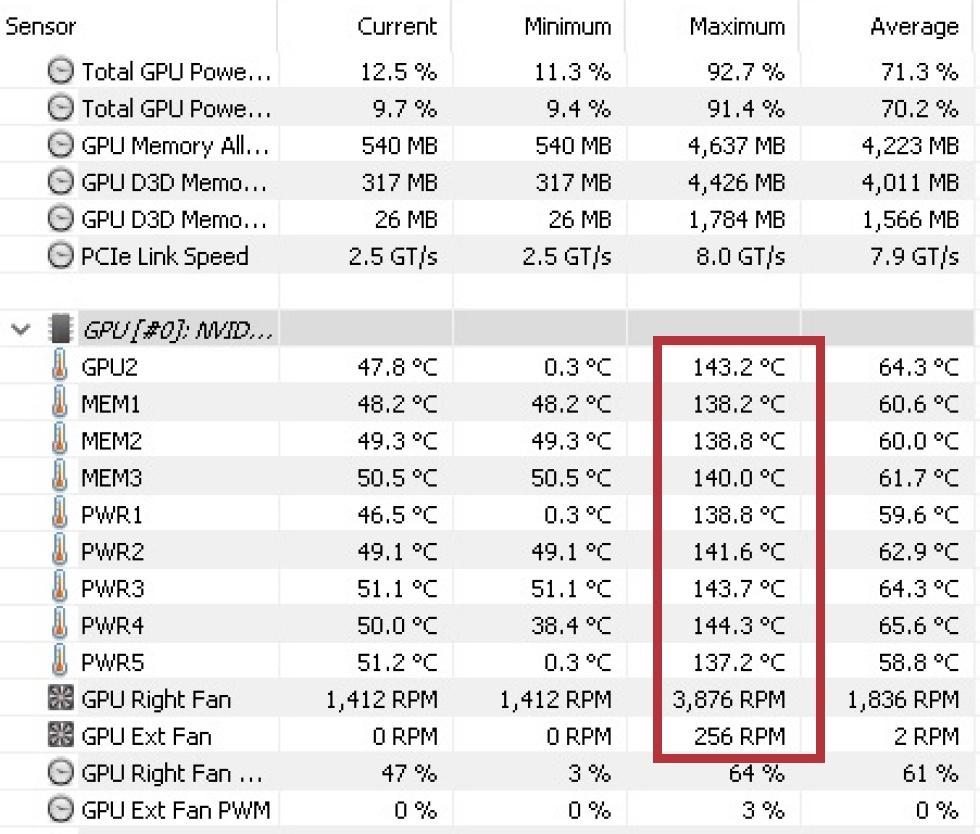
And then came the firmware update. At first glance, the values seem a little more normal, but the problem with the fan suddenly going to full capacity for no reason is still present. If we scan the ICX sensors we see the same load and the same problem, but the values it returns are slightly different, except that what can be read now is still obviously wrong.
It seems clear that the new firmware that EVGA has distributed to solve the problem is purely cosmetic, since it does not solve any problem. This is where EVGA really comes up against the challenge of having to decide what to do with your ICX technology, because obviously it doesn’t work well and if we read the values from the graphs using NVIDIA’s integrated sensors, then the values are correct.
The history of ICX and its 9 sensors
We have to look back to 2017 to see where these values come from, since the EVGA’s patented ICX technology has not changed since then. At that time it had been shown that no temperature value could be read except that of the GPU diode with the usual tools, so sometimes temperature values from VRM or others were offered in programs like GPU-Z as simple return values from the PWM controller, but they were not actual measured values.
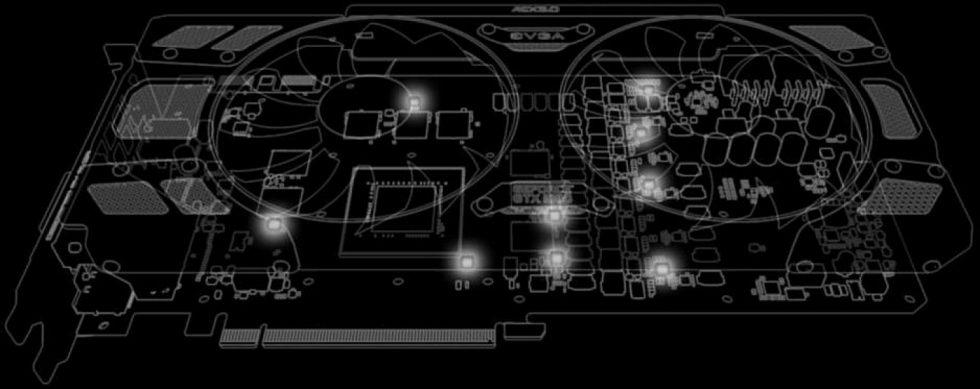
At the time, EVGA was the first manufacturer in the industry to take an unusual approach. A total of nine temperature sensors were placed at strategic points on the PCB, and since then they have been allowed to be read by software such as EVGA Precision. For fans of unconditional control, this was a true paradise, but for the normal user this did not make much sense since the truly relevant points are two or three. But if marketing smells its opportunity, so be it.
These values could also be used for fan control, such as the asynchronous control that EVGA first introduced, which is based on actual measured values in contrast to previous solutions and which made it possible to create two fan curves independent for each of the two fans. Of course, these values could only be read with the brand’s proprietary software.
Assigning the respective sensors to the fans was somewhat illogical, because the RAM is almost entirely under the left fan, while the right fan settings should affect the voltage drivers. In practice, this is exactly what happens, because the access point is right between the GPU and the VRMs. Since RAM gets considerably hotter than VRMs, the result is that you cool down the MOSFETs very much but not the memory.
The actual values measured on the memory chips
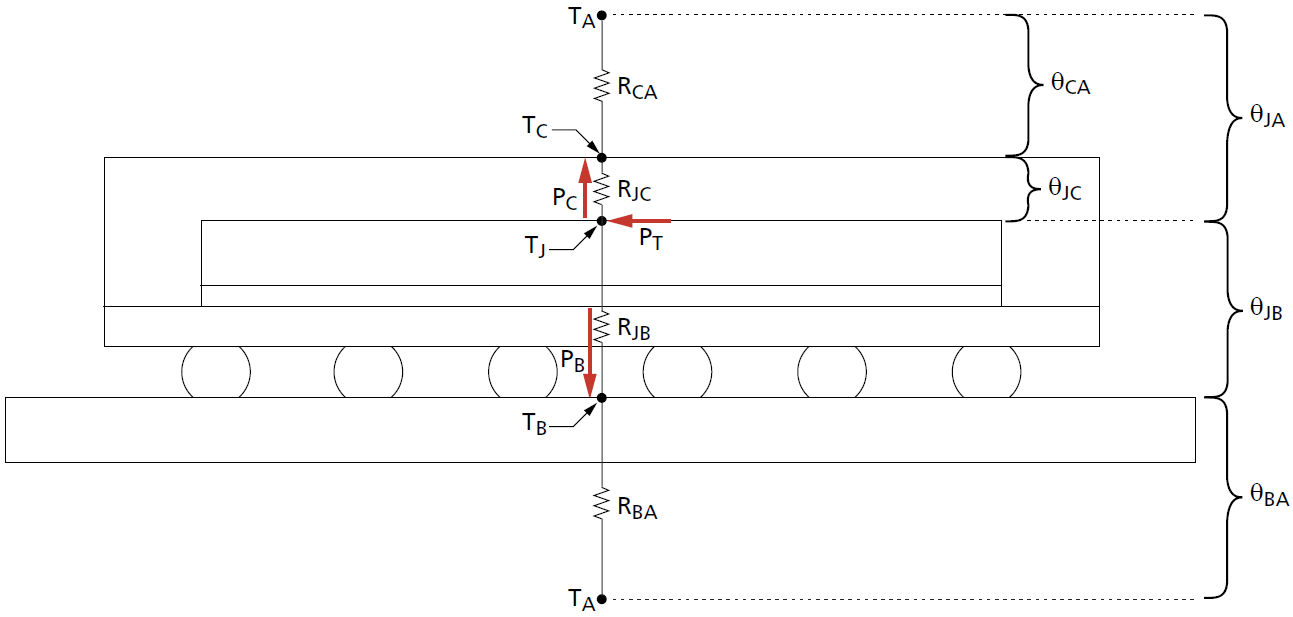
Interestingly, Micron stayed pretty tight on the NVIDIA-exclusive GDDR6 (X) memory in the first place, as even the device’s thermal information was not included in the GDDR6 documentation. Taking a look at the GDDR6X memory diagram that you can see above these lines, we can see the PT value (Maximum Power Ptot), which is supplied as electrical power and which is emitted almost entirely as generated heat.
This should be around 2.5-3 watts per module, which doesn’t seem like a lot but due to the small width of the frame and the heat density, it’s a really big heat number. Although the memory module may seem quite large, it is actually a very small chip and therefore the density of heat that must be dissipated is enormous. If the EVGA sensor has a problem reading the temperature value, things get worse because it doesn’t cool properly.
What’s the point of EVGA ICX then? How the problem is solved?
From a marketing point of view, the question is obvious since EVGA is not going to want to give up a sales incentive that no other manufacturer offers. However, since Turing NVIDIA also offers an asymmetric control of the fans, which is also based on the values determined in real time for the GPU (such as Tjunction), memory and voltage converters. This cannot be better technically solved with a patented solution based on on-board measurement points; quite the contrary, it is possible that this worsens the problem and is what is happening with the EVGA graphics.
If a faulty board design causes the MCU to be destroyed (perhaps due to overvoltage) and to display absurd reading values, then a solution as superfluous as EVGA ICX makes no sense and less so on such an expensive graphic. Nobody needs it and it also causes problems, so it doesn’t really make any sense, so it should be reason enough for EVGA to bury this relic. There are already sufficient values of the sensors of the graphs and that as we have seen they work better than the EVGA solution.
EVGA, enter the sword and the wall
EVGA is one of NVIDIA’s favorite graphics assemblers, but as a manufacturer it is not without its problems. It has always had a good reputation for the good quality of its products, as well as for its guarantee policy and customer service, but it seems that in recent times things are changing and making it worse.
For starters, in the last two generations of graphics cards it is evident that their ICX technology has become obsolete, since it does not read sensor measurements well and causes fans to run at maximum for no reason or the opposite, that does not read correct values and the graph is too hot but the fans do not work in accordance, which is causing several graphs to crash due to temperature problems.
If the GPU, VRAM, or VRM gets too hot but the sensor isn’t reading it, the fans won’t speed up to cool accordingly, and worst of all, the fans won’t jump. temperature protection systems, and this is precisely what is causing some EVGA graphics to literally burn out.
In addition to that, and despite the good reputation of its after-sales service, in this latest generation of RTX 30 Series graphics and possibly due to the shortage of chips, the manufacturer is also slightly changing its replacement policy, putting more obstacles customers and, in some cases, requesting absurd advances to change the graph through their system of Advanced RMA (In this system, the user receives a new graphic before having to send the old one, so that he never runs out of GPU) however, a few weeks ago it was learned that now EVGA requires a very high monetary advance ($ 1,800 for an RTX 3090, for example), that although later when they receive your damaged graphic they return it to you, it is still something that not many users can or are willing to face.
What is evident is that now EVGA is between the strings, and it must be the manufacturer himself who makes the next move because after the fiasco of this firmware that does not solve anything, his good reputation may go to the fret.