The rule of three is probably one of the most used “informal” mathematical operations.. In my case, I remember having learned it at school, but not from the various math teachers who came across my life as a student, no, I remember having learned it from a classmate who, in turn, had learned it from his parents. Happy for my new math skill, I didn’t hesitate to share it with other people either.
I don’t know if this will have changed at some point, since a few decades have passed since, innocent of me, when asking a teacher about said slide rule, he “invited” me to unlearn that immediately because, according to what he told me , it was a tremendously informal calculation formula, not accepted by the academic community, and that could sometimes lead to erroneous results. He seemed angry, but the truth is that this man always seemed angry, so I did not give it too much importance and, of course, I continued using the rule of three.
Over the years I came to the conclusion that, in its own way, what it was trying to tell me was that the rules of three can be direct or inverse, and that applying the direct rule of three formula when we should use the inverse (and vice versa) will always give us an erroneous result. I thank him for making me doubt, because I’m sure that was the reason why he reprimanded me for using it, and no other. That is to say, I have never ever thought that, in reality, that guy was bitter and that just behaving like that with the students calmed his vital anguish a little.
Thus, once it was clarified that that professor he was bitter wanted me to discover the difference between direct and inverse rules of three for myself, this was one of the first calculators I tried in Excel, many years ago, and I find them more useful every day. Do you want to try it yourself? Or, well, better try them, because we are going to make two calculators, one for direct rules of three and another for inverse rules of three.
Rules of three direct with Excel
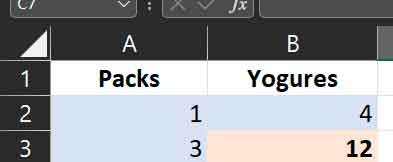
The direct rule of three is one in which there is direct proportionality, that is, when one of the magnitudes increases, the other does as well and proportionally. As a general rule, when talking about rules of three, reference is usually made to this type. Let’s take a very simple example: if a pack of yogurt contains four units, how many yogurts will I have with three packs? In this case, the operation is so simple that we can do it head first, but as the magnitudes grow and/or decimals are introduced, it may not be so simple. This is how we calculate it with Excel.
As always in these tricks, the first thing we will do is define and format the cells, leaving A2, A3 and B2 for the input of the three values that we already know, and the calculated value will be displayed in B3:
Clever? Well, he then goes to cell B3 and types the formula “= (B2 * A3) / A2” (without the quotes). Then fill in the data you already know and, immediately, Excel will return the result
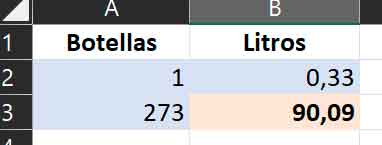
Obviously, you can use much higher orders of magnitude, decimals, etc., the calculator will work just the same
Rules of three inverses with Excel
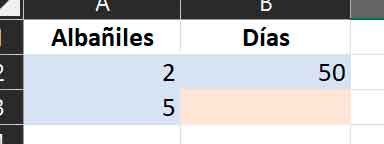
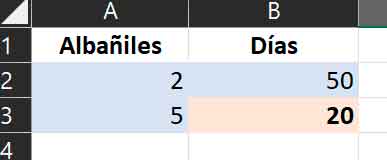
If the direct rule of three is the one in which there is direct proportionality, surely you have already deduced that in this case the proportionality is inverse, that is, when the value of one order of magnitude increases, the other decreases. Let’s say we want to do a work at home, and we know that if we have two masons, it will take 50 days. If we hire more bricklayers (magnitude that grows), the days needed will decrease (magnitude that decreases). Let’s see how to calculate it:
We will start, of course, by formatting the cells that we are going to use:
And, if we wish, we will add the data with which we want to do the calculation
Then we will go to B3 and enter the formula “=(A2*B2)/A3” (yes, exactly, without the quotes) and, immediately, we will know how many days the work will take us with more (or fewer) masons: